: Варіант 2 КР-1

Завдання № 9 КР-1 Варіант 2

Контрольна робота за І семестр (сторінка 29)

Бісектриса кута B паралелограма ABCD ділить сторону AD на відрізки AM і MD так, що AM : MD = 1 : 3. Знайдіть AD, якщо периметр паралелограма ABCD дорівнює 100 см.

А. 30 см;
Б. 40 см;
В. 45 см;
Г. 35 см.

Розв'язок:

Відповідь до завдання № 9 КР-1 вар.2 С та ДР з геометрії

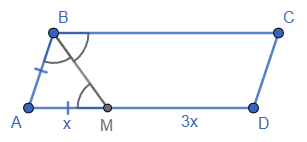
Бісектриса BM ділить кут B навпіл,
тому ∠CBM = ∠MBA (визначення бісектриси).
Оскільки AD ∥ BC,
то ∠AMB = ∠CBM (як внутрішні різносторонні кути при перетині прямої BM з паралельними BC і AD).
Отже, у △AMB маємо ∠AMB = ∠MBA,
тому AM = AB (властивість рівнобедреного трикутника).
Нехай AM = AB = x.
За умовою AM : MD = 1 : 3,
тому MD = 3x і
AD = AM + MD = 4x.
У паралелограма протилежні сторони рівні,
отже BC = AD = 4x.

Периметр паралелограма:

P = 2(AB + BC) =

= 2(x + 4x) = 10x = 100,

звідси x = 10 см.

Тоді AD = 4x = 40 см.

Відповідь:

✅Б. 40 см.