: Варіант 2 КР-1

Завдання № 7 КР-1 Варіант 2

Контрольна робота за І семестр (сторінка 28)

У прямокутній трапеції гострий кут дорівнює 60°, більша бічна сторона — 12 см, а менша основа — 5 см. Знайдіть більшу основу трапеції.

А. 9 см;
Б. 10 см;
В. 11 см;
Г. 12 см.

Розв'язок:

Нехай ABCD – задана трапеція з основами AD∥BC.
∠A = ∠B = 90°; ∠C = 60°; DC = 12 см, AD = 5 см.
Знайти: BC.

Відповідь до завдання № 7 КР-1 вар.2 С та ДР з геометрії

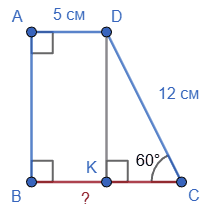
Проведемо з вершини тупого кута D перпендикуляр DK до BC.
Оскільки AB ⟂ BC і DK ⟂ BC, то AB ∥ DK (як перпендикулярні до однієї прямої).
Також AD ∥ BC, отже AD ∥ BK.
Маємо ABKD – прямокутник,
тому BK = AD = 5 см (властивість прямокутника: протилежні сторони рівні).
У △CDK кут K прямий, ∠C = 60°,
тому ∠D = 30°. За властивістю прямокутного трикутника з кутом 30° катет, що лежить проти цього кута, дорівнює половині гіпотенузи:

CK = DC : 2 = 12 : 2 = 6 см.

Тоді BC = BK + CK = 5 + 6 = 11 см.

Відповідь:

✅В. 11 см.