: Варіант 1 КР-1

Завдання № 9 КР-1 Варіант 1

Контрольна робота за І семестр (сторінка 27)

Бісектриса кута A паралелограма ABCD ділить сторону BC на відрізки BK і KC так, що BK : KC = 1 : 2. Знайдіть BC, якщо периметр паралелограма дорівнює 80 см.

А. 10 см;
Б. 20 см;
В. 30 см;
Г. 15 см.

Розв'язок:

Відповідь до завдання № 9 КР-1 вар.1 С та ДР з геометрії

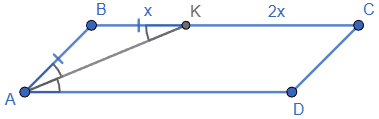
Нехай BK = x.
Тоді KC = 2x, отже BC = 3x.
AK — бісектриса кута A,
тому ∠BAK = ∠KAD (визначення бісектриси).
Оскільки AD ∥ BC (властивість паралелограма),
то ∠KAD = ∠AKB (як внутрішні різносторонні кути при перетині прямої AK з паралельними AD і BK).

Тоді ∠BAK = ∠AKB, отже △ABK рівнобедрений і AB = BK = x.
Периметр паралелограма:

P = 2(AB + BC) =

2(x + 3x) = 8x = 80,

звідси x = 10 см.

Тоді BC = 3x = 30 см.

Відповідь:

✅В. 30 см.