Завдання № 10 КР-1 Варіант 1

Контрольна робота за І семестр (сторінка 27)

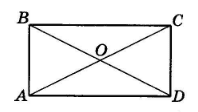
У прямокутнику ABCD діагоналі перетинаються в точці O (див. мал.). Кут OAB на 30° менший від кута AOB. Установіть відповідність між кутами (1–3) та їхніми градусними мірками (А–Г).

Кут 
1. ∠OAB;
2. ∠AOB;
3. ∠BDA;

Градусна міра кута 
А. 30°;
Б. 40°;
В. 50°; 
Г. 80°.

Розв'язок:

Нехай ∠OAB = x.
За умовою, ∠AOB на 30° більший,
тобто ∠AOB = x + 30°.
У прямокутнику діагоналі точкою перетину діляться навпіл (властивість прямокутника), тому AO = BO. Отже, △AOB рівнобедрений і ∠OAB = ∠ABO = x.

У △AOB сума кутів 180°:

x + x + (x + 30°) = 180°

3x + 30° = 180°

x = 50°.

Тому ∠OAB = 50°,

а ∠AOB = x + 30° = 80°.

Згідно властивості прямокутника, усі його кути прямі.
Розглянемо △BAD.

У ньому ∠BAD = 90°, отже трикутник прямокутний.

∠ABD = ∠ABO = 50°.

Згідно властивості прямокутного трикутника сума гострих кутів 90°:
∠ABD + ∠BDA = 90°

50° + ∠BDA = 90°

∠BDA = 40°.

Відповідь:

1. ∠OAB = 50° → В
2. ∠AOB = 80° → Г
3. ∠BDA = 40° → Б