: Варіант 3 ДР-1 [2М]

Завдання № 6 ДР-1 [2М] Варіант 3

Діагностична робота (сторінка 14)

Тема: Чотирикутник, його елементи. Паралелограм та його види

На малюнку CD = KL, ∠CDL = ∠DLK. Доведіть, що CDKL – паралелограм.

Завдання № 6 ДР 1 вар 3 Геометрія

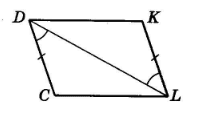
Розв’язок:

1. Розглянемо трикутники CDL і DLK. Маємо CD = KL (за умовою), DL — спільна сторона, ∠CDL = ∠DLK (за умовою). Отже, ΔCDL = ΔDLK (за двома сторонами і кутом між ними).

2. Із рівності кутів ∠CDL = ∠DLK маємо CD ∥ KL (як внутрішні різносторонні при січній DL).

3. У чотирикутнику CDKL одна пара протилежних сторін водночас рівна і паралельна (CD = KL та CD ∥ KL), отже CDKL — паралелограм (ознака паралелограма).

Відповідь:

CDKL — паралелограм.