Завдання № 6 ДР-1 [2М] Варіант 2

Діагностична робота (сторінка 13)

Тема: Чотирикутник, його елементи. Паралелограм та його види

На малюнку ∠EFN = ∠FNM, ∠FNE = ∠NFM. Доведіть, що EFMN – паралелограм.

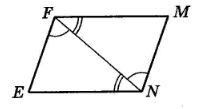
Розв’язок:

1. Розглянемо трикутники EFN і FNM. Маємо ∠EFN = ∠FNM (за умовою), FN — спільна сторона, ∠FNE = ∠NFM (за умовою). Отже, ΔEFN = ΔFNM (за ознакою подібності трикутників).

2. Із відповідності кутів: ∠EFN = ∠FNM ⇒ EF ∥ NM (як внутрішні різносторонні при січній FN).
Також ∠FNE = ∠NFM ⇒ EN ∥ FM (як внутрішні різносторонні при січній FN).

3. Протилежні сторони попарно паралельні, отже чотирикутник EFMN — паралелограм (згідно означення паралелограма).

Відповідь:

EFMN — паралелограм.