№ 9 ЗПС Геометрія = № 9 ЗПС Математика
Сторони прямокутника дорівнюють a і b (a > b). Бісектриса одного кутів прямокутника, що утворюється, утворює чотирикутник. Знайдіть його діагоналі.
Розв'язок:
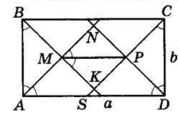
△AND — рівнобедрений, оскільки ∠NAD = ∠NDA = 45°.
Тому AN = ND.
△ABM = △DPC за стороною і прилеглими кутами (AB = CD = b, ∠MBA = ∠BAM = ∠PCD = ∠CDP =45°).
Звідси AM = PD. Тоді MN = NP.
Аналогічно MK = KP. ∠NMK = 90° як вертикальний до кута BMD.
Отже, MNPK — квадрат.
∠NMP = 45°,
∠NMP = ∠MAD, а ці кути є відповідними при прямих MP і AD і січній AM.
Тоді MP ∥ AD.
Аналогічно можна довести, що AN ∥ KC.
AMPS — паралелограм.
MP = AS = AD – DS = a – b
(△SCD — прямокутний і рівнобедрений, SD = CD = b).
NK = MP = a − b.
Відповідь:
a − b.
