Завдання № 5

№ 5 ЗПС Геометрія = № 5 ЗПС Математика

Діагоналі опуклого чотирикутника розбивають його на чотири трикутники, периметри яких однакові. Визначте вид чотирикутника.

Розглянемо два випадки.

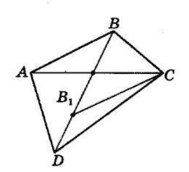
1. Точка O — середина однієї діагоналі і не є серединою іншої діагоналі.

Нехай AO = OC, BO < OD.

Позначимо на відрізку OD точку B₁, так, що OB₁ = OB.

Оскільки △ABO ∼ △CB₁O (за двома сторонами і кутом між ними: AO = CO.

BO = B₁O, ∠AOB = ∠COB₁ (як вертикальні), то AB = CB₁.

За умовою P_△ABO = P_△CDO,

або AB + AO + OB =

= OB₁ + BD₁ + DC + CO.

Звідси, враховуючи, що

AO = OC і OB = OB₁, отримаємо, що

AB = B₁D + DC

або CB₁ = B₁D + DC.

Але в △CB₁D CB₁ < B₁D + DC. Отримали суперечність, значить, перший випадок неможливий.

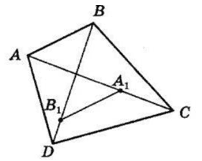
2. Точка O не є серединою жодної з діагоналей.

Нехай AO < OC, BO < OD.

Позначимо точки A₁ і B₁ на відрізках OC і OD, так, що

OA₁ = OA, OB₁ = OB, і розглянемо △OA₁B₁.

Оскільки △AOB = △A₁OB₁, то AB = A₁B₁.

За умовою P_△ABO = P_△CDO

або AB + AO + OB =

= OB₁ + B₁D + DC + CA₁A₁O.

Звідки, враховуючи рівності OA₁ = OA і OB = OB₁,

отримаємо

AB = B₁D + DC + CA₁ або

A₁B₁ = B₁D + DC + CA₁.

Але в чотирикутнику

A₁B₁DC A₁B₁ < B₁D + DC + CA₁.

Отримали суперечність, значить, випадок 2 також не може бути.

Отже, AO = OC, BO = OD, тому ABCD — паралелограм. А з умови P_△AOB = P_△COB випливає, що AB = BC, тобто сусідні сторони паралелограма рівні.

Тоді ABCD — ромб.

ромб.