№ 41 ЗПС Геометрія = № 41 ЗПС Математика
AD і BC – основи трапеції ABCD, CD = c. Точка K – середина більшої сторони AB. Відстань від точки K до прямої, що містить сторону CD, дорівнює d. Знайдіть площу трапеції.
Розв'язок:
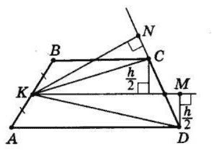
Проведемо відрізок KM паралельно основам трапеції. Оскільки K — середина AB, то M — середина CD, KM — середня лінія трапеції.
Вона ділить висоту трапеції $h$ навпіл, значить, висоти трикутників $KCM$ і $KMD,$ проведені до сторони $KM,$ дорівнюють $\frac{h}{2}.$
$S_{\triangle KCD} = S_{\triangle KCM} + S_{\triangle KMD} =$
$= \frac{1}{2} KM \cdot\ \frac{h}{2} + \frac{1}{2} KM \cdot \frac{h}{2} =$
$= \frac{1}{2} KM \cdot\ h = \frac{1}{2} \cdot \frac{AD + BC}{2} h =$
$= \frac{1}{2}S_{ABCD}.$
$S_{ABCD} = 2S_{\triangle KCD} =$
$= 2(S_{\triangle KND} - S_{\triangle KNC}) =$
$= 2(\frac{1}{2} KN ⋅ ND\ – $
$– 12 KN ⋅ NC) =$
$= 2 ⋅ \frac{1}{2}(d ⋅ (c + NC)\ –$
$ – d ⋅ NC) =$
$= dc + d ⋅ NC – d ⋅ NC = dc.$
Відповідь:
$dc.$
