№ 40 ЗПС Геометрія = № 40 ЗПС Математика
Бісектриси всіх кутів трапеції перетинаються в точці O, яка міститься на відстані d від більшої сторони трапеції. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють m і n.
Розв'язок:
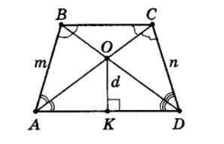
Точка перетину O всіх бісектрис трапеції $ABCD$ — це центр вписаного кола, тоді $OK ⊥ AD$ — радіус цього кола, $OK = d,$ а висота трапеції дорівнює $2d.$
Оскільки в трапецію вписано коло, то сума основ дорівнює сумі бічних сторін $m + n.$
$S_{ABCD} = \frac{m + n}{2} ⋅ 2d = $
$= (m + n)d.$
Відповідь:
$(m + n)d.$
