№ 42 ЗПС Геометрія = № 42 ЗПС Математика
У трапеції ABCD M – середина більшої основи AD, AB = BC = CD = a. Точка перетину діагоналей трапеції збігається з точкою перетину висот трикутника BMC. Знайдіть площу трапеції.
Розв'язок:
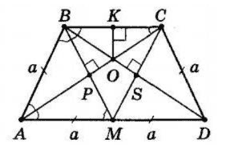
$O$ — точка перетину діагоналей і точка перетину висот трикутника $BMC.$
У $△ABC ∠BAC = ∠BCA$ (кути при основі).
$∠BCA = ∠CAD$ як внутрішні різносторонні при паралельних прямих $BC$ і $AD$ та січній $AC.$
Отже, $AC$ — бісектриса кута $A,$ але діагональ $AC$ містить висоту $CP (CP ⊥ BM).$
Отже, в $△ABM\ AB = AM = a,$
$ MD = AM = a.$
$ABCM$ — ромб $(BM ⊥ AC),$
тоді $MC = AB = a.$
Аналогічно, $BM = CD = a.$
Отже, $△ABM = △BMC =$
$= △CMD$ — рівносторонні.
Площа кожного дорівнює $\frac{a^2\sqrt3}{4}.$
$S_{ABCD} = 3 ⋅ \frac{a^2\sqrt3}{4} = \frac{3a^2\sqrt3}{4}$.
Відповідь:
$\frac{3a^2\sqrt3}{4}$.
