№ 39 ЗПС Геометрія = № 39 ЗПС Математика
На сторонах AB, BC, AC трикутника ABC позначено точки M, K, P так, що AM : MB = BK : KC = CP : PA = 2 : 1. Площа трикутника ABC дорівнює S. Знайдіть площу чотирикутника APKM.
Розв'язок:
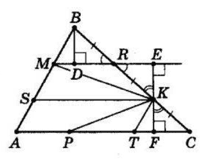
Поділимо кожну сторону трикутника ABC на три рівних частини і позначимо точки M, K і P так, що AM : MB =
= BK : KC = CP : AP = 2 : 1.
Проведемо MR (BR = RK) і висоти трикутників MBR і MTK:
BD ⊥ MR, KE ⊥ MR.
△BDR = △KER за гіпотенузою і гострим кутом
(BR = RK, ∠BRD = ∠ERK як вертикальні).
Тоді BD = KE.
S△MBR = $\frac{1}{2}$ MR ⋅ BD;
S△MRK = $ \frac{1}{2}$ MR ⋅ EK,
тому S△MBR = S△MRK.
Проведемо KT (PT = CT) і KF ⊥ AC — висоту трикутників PKT і TKC.
△REK = △CFK за гіпотенузою і гострим кутом
(RK = KC, ∠RKE = ∠CKF як вертикальні).
Тоді KF = EK.
Отже, KF = KE = BD.
S△PKT = $\frac{1}{2}$ PT ⋅ KF;
S△TKC = $ \frac{1}{2}$ TC ⋅ KT.
Оскільки PT = TC = $ \frac{1}{3}$ AC,
то S△PKT = S△TKC.
△MBR ∼ △SBK ∼ △ABC за двома сторонами і кутом B між ними.
Тоді BD = KE = KF = $ \frac{1}{2}$h
(h — висота △ABC, проведена до сторони AC),
MR = PT = TC = $\frac{1}{3}$ AC.
S△MBR = S△MRK = S△PKT = S△TKC =
= $\frac{1}{2}$ ⋅ $\frac{1}{3}$ AC ⋅ $\frac{1}{3}$h = $\frac{1}{18}$ AC ⋅ h =
= $ \frac{1}{9}$ S.
SAMKP = S – 4 ⋅ $\frac{1}{9}$ S = $\frac{5}{9}$ S.
Відповідь:
$\frac{5}{9}$ S.
