№ 38 ЗПС Геометрія = № 38 ЗПС Математика
На сторонах AB, BC, AC трикутника ABC позначено точки M, K, P так, що AM : MB = BK : KC = CP : PA = 2 : 1. Площа трикутника ABC дорівнює S. Знайдіть площу чотирикутника APKM.
Розв'язок:
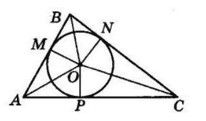
Точка перетину бісектрис кутів трикутника O є центром вписаного кола.
OM ⊥ AB, ON ⊥ BC, OP ⊥ AC — відстані від точки O до сторін трикутника.
OM = ON = OP = 3 см, як радіуси вписаного кола.
S△ABC = S△AOC + S△AOB +
+ S△BOC = $\frac{1}{2}$AC ⋅ OP +
+ $\frac{1}{2}$ AB ⋅ OM + $ \frac{1}{2}$ BC ⋅ ON =
= $\ \frac{1}{2}$ OP ⋅ (AB + BC + AC) =
= $\frac{1}{2}$ OP.
P△ABC = $\frac{1}{2}$ ⋅ 3 ⋅ 36 = 54 (см2).
Відповідь:
54 см2.
