№ 36 ЗПС Геометрія = № 36 ЗПС Математика
У скільки разів площа трикутника ABC більша за площу трикутника ABM, де M – точка перетину медіан трикутника ABC?
Розв'язок:
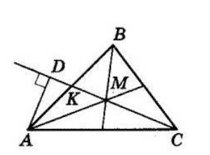
Доведемо, що площа кожного з шести трикутників, на які медіани розбивають трикутник ABC, дорівнює $\frac{1}{6}$ площі △ABC.
Розглянемо △ABM. Опустимо з вершини A перпендикуляр AD на пряму CK.
Тоді S△AKM = $\frac{1}{2}$ MK ⋅ AD = $\frac{1}{2}$ ⋅ $\frac{1}{3}$ KC ⋅ AD = $\frac{1}{3}$ S△AKC
(за властивістю медіани CM : MK = 2 : 1).
Оскільки медіана ділить △ABC на два трикутники з рівними площами, то S△AKC = S△BKC.
S△AKM = $\frac{1}{2}$ ⋅ $\frac{1}{3}$ S△ABC = $\frac{1}{6}$ S△ABC.
Тоді S△ABM = 2S△AMK =
= 2 ⋅ $\frac{1}{6}$ S△ABC= $\frac{1}{3}$ S△ABC.
Відповідь:
у 3 рази.
