№ 35 ЗПС Геометрія = № 35 ЗПС Математика
Усередині прямокутного трикутника ABC (∠C = 90°) взято точку M так, що площі трикутників AMB, BMC і CMA рівні між собою. Доведіть, що MA2 + MB2 = 5MC2.
Розв'язок:
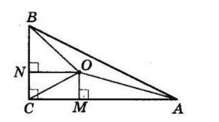
Проведемо перпендикуляри OM і ON до прямих AC і BC.
Нехай площа трикутника ABC дорівнює S.
За умовою S△AOC = $\frac{1}{3}$ S або
$\frac{1}{2}$ OM ⋅ AC = $\frac{1}{3}$ ⋅ $\frac{1}{2}$ AC ⋅ BC.
Звідси випливає, що:
OM =$\frac{1}{3}$ BC.
Аналогічно доводимо, що
ON = $\frac{1}{2}$ AC.
CM = $\frac{1}{3}$ AC,
тому AM = AC – CM = $\frac{2}{3}$ AC.
Аналогічно,BN = $\frac{2}{3}$ BC.
За теоремою Піфагора:
з △AOM OA2= OM2 + MA2 =
= $\frac{1}{9}$ BC2 + $\frac{4}{9}$ AC2;
з △BON OB2 = ON2 + NB2 =
= $\frac{1}{9}$ AC2 + $\frac{4}{9}$ BC2;
з △COM OC2 = OM2 + MC2 =
= $\frac{1}{9}$ BC2 + $\frac{1}{9}$ AC2.
З цих рівностей випливає, що OA2 + OB2 = 5 ⋅ OC2.
