№ 30 ЗПС Геометрія = № 30 ЗПС Математика
ABCD – прямокутник, у якого ∠A = B = 90°, AB = a, CD = b, BC = c, BC < DA. Знайдіть відстань від точки B до прямої, що містить CD.
Розв'язок:
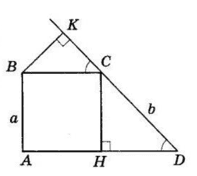
Проведемо $CH ⊥ AD.$
$ABCH$ — прямокутник, тому $CH = AB = a.$
$ΔBKC ∼ ΔCHD (∠BKC = ∠CHD = 90°),$
$∠KCB = ∠CDH$ — відповідні кути при паралельних прямих $BC$ і $AD$ та січній $CD.$
З подібності трикутників випливає, що:
$\frac{BK}{BC}\ =\ \frac{CH}{CD},$
звідки $BK = \ \frac{CH ⋅ BC}{BC}.$
$BK\ =\ \frac{ac}{b}.$
Відповідь:
$\frac{ac}{b}.$
