Завдання № 28

№ 28 ЗПС Геометрія = № 28 ЗПС Математика

У прямокутний трикутник вписано коло. Точка дотику ділить гіпотенузу у відношенні 2 : 3. Знайдіть периметр трикутника, якщо центр вписаного кола міститься на відстані m√2 від вершини прямого кута.

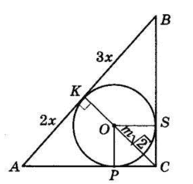
Точка $K$ ділить гіпотенузу $AB$ так, що:

$AK : KB = 2 : 3.$

Тоді $AK = 2x, BK = 3x.$

Проведемо $OS ⊥ BC$ і $OP ⊥ AC$ — радіуси в точки дотику кола з катетами.

$POSC$ − квадрат, $OC = m\sqrt{2}$ − його діагональ.

Тоді $PC = SC = m.$

За властивістю дотичних, проведених до кола з однієї точки,

$AP = AK = 2x,$

$BS = BK = 3x.$

За теоремою Піфагора:

$AB^2 = AC^2 + BC^2;$

$(2x + 3x)^2 = $

$= (2x + m)^2 + (3x + m)^2;$

$25x^2 = 4x^2 + 4xm + m^2 + $

$+ 9x^2 + 6xm + m^2;$

$12x^2 − 10xm − 2m^2 = 0;$

$6x^2 − 5xm − m^2 = 0;$

$D = (−5m)^2 – 4 ⋅ 6 ⋅ (−m) = $

$= 25m^2 + 24m^2 = 49m^2;$

$x_1\ =\ \frac{5m\ +\ \sqrt{49m^2}}{12}\ =$

$= \ \frac{5m\ +\ 7m}{12}\ =\ m;$

$x_2\ =\ \frac{5m\ −\ \sqrt{49m^2}}{12} < 0$ —

не задовольняє умові.

Отже, $AB = 5m;$

$AC = 2m + m = 3m; $

$BC = 3m + m = 4m.$

$P_{△ABC} = 5m + 3m + 4m =$

$= 12m.$

$12m.$