Завдання № 27

№ 27 ЗПС Геометрія = № 27 ЗПС Математика

1) У гострокутному трикутнику ABC BH – висота. Доведіть, що BC² = AB² + AC² − 2AC · AH.  
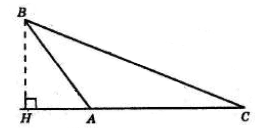
2) У трикутнику ABC ∠A – тупий, BH – висота. Доведіть, що BC² =
= AB² + AC² + 2AC · AH. 

Розв'язок:

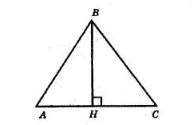
1. З ΔABH BH² = AB² − AH².

З ΔCBH BH² = BC² − CH² =

= BC² − (AC − AH)² =

= BC² − AC² + 2AC ⋅ AH − AH².

Ліві частини рівностей однакові, тому 

AB² – AH² =

= BC² – AC² + 2AC ⋅ AH − AH²;

BC² = AB² – AH² + AC² –

– 2AC ⋅ AH + AH²;

BC² = AB² + AC² – 2AC ⋅ AH. 

2. З ΔABH BH² = AB² − AH².

З ΔBCH BH² =

= BC² – (AH + AC)² =

= BC² − AH² – 2AH ⋅ AC – AC².

AB² – AH² =

= BC² – AH² – 2AH ⋅ AC – AC²;

BC² = AB² – AH² + AH² +

+ 2AH ⋅ AC + AC²;

BC² = AB² + AC² + 2AC ⋅ AH.