Завдання № 25

№ 25 ЗПС Геометрія = № 25 ЗПС Математика

Точка M лежить усередині кута, який дорівнює 60°. Відстані від точки M до сторін кута дорівнюють a і b. Знайдіть відстань від точки M до вершини кута.

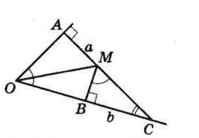
Нехай $MA$ і $MB$ — перпендикуляри, проведені до сторін кута — відстані до них від точки $M.$

Продовжимо $AM$ до перетину з $OB$ у точці $C.$

$ΔAOC ∼ ΔBMC$ ($∠C$ спільний кут), трикутники прямокутні.

Тоді $\frac{AO}{BM} = \frac{AC}{BC};$

$∠CMB = ∠COA = 60°.$

З $ΔBMC\ BC = BM\ tg 60° =$

$= b\sqrt{3}.$

$MC = 2BM = $

$= 2b(∠C = 90° − 60° = 30°).$

$AC = AM + MC = a + 2b.$

Отже, $AO = \frac{BM ⋅ AC}{BС} = \frac{b(a + 2b)}{b\sqrt{3}} =$

$= \frac{a + 2b}{b\sqrt{3}}.$

З $ΔAOM\ OM =$

$= \sqrt{AM^2 + OA^2} =$

$= \sqrt{a^2 + \frac{(a + 2)^2}{(\sqrt{3})^2}} =$

$= \sqrt{a^2 + \frac{a^2 + 4ab+4b^2}{3}} =$

$= \sqrt{\frac{3a^2+a^2 + 4ab+4b^2}{3}} =$

$= 2\sqrt{\frac{a^2 + ab+b^2}{3}}.$

$2\sqrt{\frac{a^2 + ab+b^2}{3}}.$