Завдання № 24

№ 24 ЗПС Геометрія = № 24 ЗПС Математика

Діагоналі чотирикутника ABCD взаємно перпендикулярні. Доведіть, що AD² + BC² = AB² + CD².   

Розв'язок:

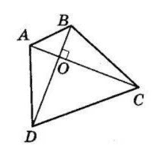
За умовою AC ⊥ BD, O — точка перетину діагоналей.

З ΔAOB AB² = AO² + BO².

З ΔCOD CD² = CO² + DO².

Додамо ці рівності:

AB² + CD² =

= AO² + BO² + CO² + DO². (1)

З ΔAOD AD² = AO² + DO².

З ΔBOC BC² = BO² + CO².

Додамо ці рівності:

AD² + BC² =

= AO² + BO² + CO² + DO². (2)

Праві частини рівностей (1) і (2) рівні, то ліві також рівні:

AB² + CD² = AD² + BC².