№ 21 ЗПС Геометрія = № 21 ЗПС Математика
Через середину найбільшої сторони трикутника проведено пряму, яка відтинає від нього трикутник, подібний даному. Знайдіть найменшу сторону трикутника, що відтинається, якщо сторони даного дорівнюють:
1. 42 см; 49 см; 56 см;
2. 42 см; 49 см; 63 см;
3. 42 см; 49 см; 70 см.
Скільки розв’язків має задача в кожному з випадків?
Розв'язок:
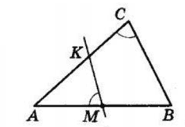
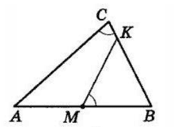
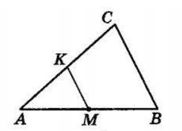
I випадок.
$MK$ перетинає $BC$ і $MK || AC.$
$△ACB ∼ △MKB.$ Тоді найменша сторона трикутника $MKB$ дорівнює половині найменшої сторони
трикутника $ ABC,$ тобто половині $AC,$ а саме:
1. $21$ см;
2. $21$ см;
3. $21$ см.
II випадок.
$MK$ перетинає $AC$ і $MK || BC.$
$△AKM ∼ △ACB.$ В цьому випадку також найменша сторона $ΔAKM$ дорівнює половині $AC.$
III випадок.
$MK$ перетинає $BC,$ проте $MK$ не паралельна $AC,$
тоді $∠C = ∠KMB$ і $△ABC ∼ △KBM.$
$\frac{AB}{KB}\ =\ \frac{AC}{KM}\ =\ \frac{BC}{BM};$ найменша – $KM.$
1. $\frac{56}{KB}\ =\ \frac{42}{KM}\ =\ \frac{49}{28};$
$KM = 24$ см; $KB = 32$ см.
2. $\frac{63}{KB}\ =\ \frac{42}{KM}\ =\ \frac{49}{31,5};$
$KM = 27$ см; $KB = 40{,}5$ см.
3. $\frac{70}{KB}\ =\ \frac{42}{KM}\ =\ \frac{49}{35};$
$KM = 30$ см; $KB = 50$ см.
Але $KB < CB.$ Тому неможливо $KB = 50$ см.
IV випадок.
$MK$ перетинає $AC,$ проте $MK$ не паралельна до $BC.$
Тоді $∠AKM = ∠B$ і $△AKM ∼ △ABC.$
$\frac{AK}{AB}\ =\ \frac{AM}{AC}\ =\ \frac{KM}{BC}.$
1. $\frac{AK}{56}\ =\ \frac{28}{42}\ =\frac{KM}{49};$
$AK\ =\ 37\frac{1}{3}$ см; $KM = 32\frac{2}{3}$ см.
$AM = 28$ см — найменша сторона $△AKM.$
2. $\frac{AK}{63}\ =\ \frac{31,5}{42}\ =\ \frac{KM}{49};$
$AK = 47{,}25$ см. Це неможливо,
оскільки $AC = 42$ см.
3. $\ \frac{AK}{70}\ =\ \frac{35}{42}\ =\ \frac{KM}{49};$
$AK\ =\ 58\frac{1}{3}$ см.
Це неможливо, оскільки $AC = 42$ см.
Відповідь:
1. $21$ см або $24$ см або $28$ см;
2. $21$ см або $27$ см;
3. $21$ см.
