Завдання № 2

№ 2 ЗПС Геометрія = № 2 ЗПС Математика

На основі AB рівнобедреного трикутника ABC взято довільну точку K. Через цю точку паралельно BC і AC проведено прямі, які перетинають сторони трикутника. Доведіть, що периметр паралелограма, який при цьому утворився, не залежить від положення точки K.

Розв'язок:

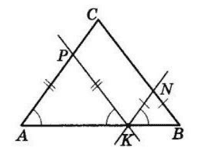
У ΔABC AC = BC, ∠A = ∠B, 

K ∈ AB, PK ∣∣ BC, KN ∣∣ AC.

∠PKA=∠B як відповідні при паралельних прямих PK і BC та січній AB.

Тоді в ΔAPK

∠A = ∠PKA, 

тому AP = PK.

∠NKB = ∠A як відповідні при паралельних прямих NK і AC і січній AB.

Тоді ΔKNB ∠NKB = ∠B, тому NK = NB.

P_PCNK = PC + CN + NK + PK =

= PC + AP + CN + NB = AC + BC.

Таким чином, периметр не залежить від положення точки K.