№ 1 ЗПС Геометрія = № 1 ЗПС Математика
На сторонах AB і CD паралелограма ABCD зовні нього побудовано два рівносторонніх трикутники ABK і CDL. Доведіть, що відрізок KL проходить через точку перетину діагоналей паралелограма.
Розв'язок:
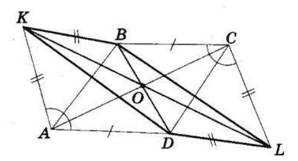
Розглянемо чотирикутник KBLD.
ΔBCL = ΔDAK за двома сторонами і кутом між ними:
BC = AD як протилежні сторони паралелограма,
CL = AK = AB = CD за побудовою;
∠BCL = ∠BCD + 60°,
∠KAD = ∠BAD + 60°,
∠BCD=∠BAD як протилежні.
З рівності трикутників BL = KD. KB = DL як сторони рівних рівносторонніх трикутників.
Отже, KBLD — паралелограм (протилежні сторони попарно рівні).
Тоді діагоналі BD і KL перетинаються в точці, що є серединою кожної з них, значить, KL проходить через середину діагоналі BD, а це і є точка перетину діагоналей паралелограма ABCD.
