№ 16 ЗПС Геометрія = № 16 ЗПС Математика
Діагоналі чотирикутника ABCD, вписаного в коло, перетинаються в точці M. Відомо, що ∠ABC = 73°, ∠BCD = 103°, ∠AMD = 110°. Знайдіть ∠ACD.
Розв'язок:
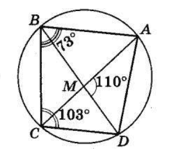
Кут, вершина якого лежить усередині кола, вимірюється півсумою двох дуг, одна з яких міститься між його сторонами, а інша — між продовженням сторін.
$ᴗBAD = 2∠BCD = $
$= 2 · 103° = 206°.$
$ᴗADC = 2∠ABC = $
$= 2 · 73° = 146°$
Шуканий кут $∠ACD$ вимірюється половиною дуги, на яку він спирається:
$\angle ACD\ =\ \frac{ᴗAD}{2}.$
$∠AMB = 180° − ∠AMD = $
$= 180° − 110° = 70°.$
Але $∠AMB = \ \frac{ᴗAB + ᴗCD}{2}.$
Визначимо дугу
$ᴗAD: ᴗAD = $
$= ᴗBAD − ᴗAB $
або $ᴗAD = ᴗADC − ᴗCD.$
Додамо ці рівності:
$2ᴗAD = ᴗADC + ᴗBAD −$
$ − (ᴗAB + ᴗCD),$
але $ᴗAB + ᴗCD = $
$= 70° · 2 = 140°,$
а $ᴗADC + ᴗBAC = $
$= 206° + 146° + 352°.$
Тоді $2ᴗAD = 352° − 140° =$
$= 212°,\ ᴗAD = 106°.$
$\angle ACD\ =\ \frac{1}{2}\ ᴗAD =$
$= \ \frac{1}{2} · 106° = 53°.$
Відповідь:
$53°$
