№ 15 ЗПС Геометрія = № 15 ЗПС Математика
Основи трапеції дорівнюють a і b (a > b), а сума кутів, прилеглих до більшої основи, дорівнює 90°. Знайдіть відстань між серединами основ трапеції.
Розв'язок:
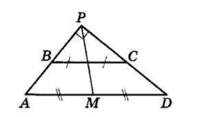
Продовжимо бічні сторони трапеції до їх перетину в точці $P.$
За умовою в трикутнику $△APD\ ∠A + ∠D = 90°,$
тому $∠P = 90°.$
$PM$ — медіана, проведена з вершини прямого кута.
$PM\ =\ \frac{1}{2}AD\ =\ AM\ =$
$= MD\ =\ \frac{a}{2}.$
$△BPC ∼ △APD$ за гострим кутом
($∠PAD = ∠PBC$ як відповідні при $BC ∥ AD$ і січній $AP$).
Отже, $\frac{BC}{AD} = \frac{PK}{PM}.$
Позначимо $KM = x,$
тоді $PK = \frac{a}{2} – x.$
$\frac{b}{a}\ = \ \frac{\frac{a}{2} –x}{\frac{a}{2}};$
$\frac{ab}{2}\ = \frac{a^2}{2} – ax;$
$ax\ =\ \frac{a^2– ab}{2};$
$x\ =\ \frac{a– b}{2}.$
Отже, $KM = \ \frac{a– b}{2}.$
Відповідь:
$\ \frac{a– b}{2}.$
