ВПР 4 №33 Геометрія = ВПТ 10 №33 Математика
EF – середня лінія трикутника ABC, EF || AB. У скільки разів площа трикутника CEF менша за площу трапеції AEFB?
Розв'язок:
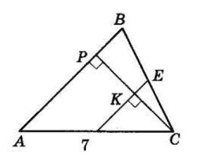
$EF$ — середня лінія $ΔABC, $
$EF ∣∣ AB, EF = \frac{1}{2} AB.$
Тоді $AB = 2EF. $
$ΔFEC ∼ ΔABC,$ тоді їх відповідні елементи (сторони, висоти тощо) пропорційні.
$\frac{CF}{AC}\ =\ \frac{CE}{BC}\ =\ \frac{FE}{AB}\ =$
$= \ \frac{CK}{CP}\ =\ \frac{1}{2},$
тоді $KP = CK.$
$S_{\Delta FEC}=\ \frac{1}{2}\ EF\ \cdot\ CK;$
$S_{ABEF}=\ \frac{EF\ +\ AB}{2}\cdot\ PK\ =$
$= \ \frac{EF\ +\ 2EF}{2}\ \cdot\ CK\ =$
$= \frac{1}{2}\ EF\ \cdot\ CK.$
$S_{ABEF}\ =\ \frac{\frac{3}{2}\ EF\ \cdot\ CK}{\frac{1}{2}\ EF\ \cdot\ CK}\ =\ \frac{3}{1}.$
Відповідь:
у $3$ рази.
