ВПР 4 №32 Геометрія = ВПТ 10 №32 Математика
Обчисліть площу прямокутної трапеції, у якої дві менші сторони дорівнюють по b см, а гострий кут – 45°.
Розв'язок:
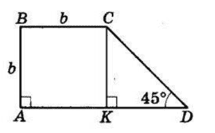
$ABCD$ — трапеція, $AB ⊥ AD, CK ⊥ AD$ — висота.
$AB = BC = b$ см, $∠D = 45°.$
$CK = AB = b$ см
$ΔCKD$ — прямокутний і рівнобедрений $(∠D = 45°),$
тоді $KD = CK = b$ см.
$AK = BC = b$ см ($ΔBCK$ — квадрат).
$S_{ABCD}=\ \frac{BC\ +\ AD}{2}\cdot\ AB\ =$
$=\ \frac{b\ +\ 2b}{2}\cdot\ b\ =\ \frac{3b^2}{2}$ (см2).
Відповідь:
$\frac{3b^2}{2}$ см2.
