Завдання № 34

ВПР 4 №34 Геометрія =  ВПТ 10 №34 Математика

У рівнобічну трапецію вписано коло, яке ділить бічну сторону на відрізки завдовжки 2 см і 8 см. Знайдіть площу трапеції.

Розв'язок:

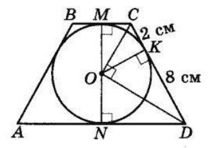
Проведемо через центр вписаного кола висоту $MN.$

$OK ⊥ CD$ — радіус, проведений в точку дотику.

$CK = 2$ см, $ KD = 8$ см.

За властивістю відрізків дотичних, проведених з однієї точки,

$CK = MC = 2$ см, $ND = KD = 8$ см.

$M$ — середина $BC, N$ — середина $AD,$

$BC = 2MC = 2 ⋅ 2 = 4$ (см),

$AD = 2ND = 2 ⋅ 8 = 16$ (см).

$ΔCOD$ — прямокутний, оскільки

$∠OCD + ∠ODC = $

$= \frac{1}{2} ∠C + \frac{1}{2} ∠D =$

$= \frac{1}{2} (∠C + ∠D) =$

$= \frac{1}{2} ⋅ 180° = 90°.$

$OK^2 = CK ⋅ KD;$

$OK = \sqrt{2\ \cdot\ 8\ } = \sqrt{16\ } = 4$ (см).

$MN = 2OK = 2 ⋅ 4 = 8$ (см).

$S_{ABCD} = \frac{AD + BC}{2}⋅ MN =$

$= \frac{4 + 16}{2} ⋅ 8 = 80$ (см²).

Відповідь:

$80$ см².