ВПР 4 №31 Геометрія = ВПТ 10 №31 Математика
Висоти, проведені з вершин меншої основи рівнобічної трапеції, ділять більшу основу на три відрізки, сума двох з яких дорівнює третьому. Знайдіть площу трапеції, якщо її менша основа й висота дорівнюють по a см.
Розв'язок:
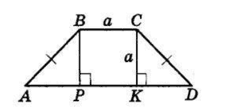
$ABCD$ — трапеція,
$BC || AD, AB = CD.$
$BP ⊥ AD, CK ⊥ AD$ — висоти,
$BC = BP = CK = a$ см.
Оскільки $AP = KD,$
то $AP + KD = PK.$
$PBCK$ — прямокутник
$(PB || CK, PB = CK, $
$BP ⊥ PK).$
Тоді $PK = a$ см,
значить, $AP = KD = \frac{1}{2}PK = \frac{a}{2}$ (см).
$AD\ =\ \frac{a}{2}+ a + \frac{a}{2} = 2a$ (см).
$S_{ABCD}\ =\ \frac{BC\ +\ AD}{2}\ \cdot\ CK\ =$
$= \ \frac{a+2a}{2}\cdot\ a =\ \frac{3a^2}{2}$ (см2).
Відповідь:
$\ \frac{3a^2}{2}$ см2.
