ВПР 4 №21 Геометрія = ВПТ 10 №21 Математика
У паралелограмі ABCD гострий кут дорівнює 30°, а бісектриса цього кута, перетинаючи сторону, ділить її навпіл. Знайдіть площу паралелограма, якщо його периметр дорівнює 24 см.
Розв'язок:
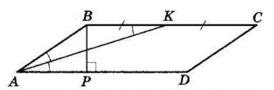
$ABCD$ — паралелограм, $∠A = 30°, AK$ — бісектриса кута $A, BK = KC.$
$∠BKA = ∠KAD$ як внутрішні різносторонні при паралельних прямих $AD$ і $BC$ та січній $AK.$
Але $∠BAK = ∠KAD$ за умовою.
Тоді $∠BAK = ∠BKA. $
$ΔABK$ — рівнобедрений з основою $AK, AB = BK.$
За умовою $BK = KC,$ тоді $BC = 2AB.$
$P_{ABCD} = 2(AB + BC) =$
$= 2(AB + 2AB) =$
$= 2 · 3AB = 6AB.$
За умовою $6AB = 24$ см, отже $AB = 4$ см.
$BC = 2AB = 2 · 4 = 8$ (см).
$BP ⊥ AD$ — висота паралелограма.
З $ΔABP\ sin ∠A = \frac{BP}{AB};$
$BP\ =\ AB\ · sin ∠A =$
$= 4\ sin 30° = 4 \frac{1}{2} = 2$ (см).
$S_{ABCD} = AD · BP = $
$= BC · BP = 8 · 2 = 16$ (см2).
Відповідь:
16 см2.
