ВПР 4 №20 Геометрія = ВПТ 10 №20 Математика
Квадрат і ромб мають рівні між собою сторони, а тупий кут ромба дорівнює 150°. Яка з фігур має більшу площу? У скільки разів?
Розв'язок:
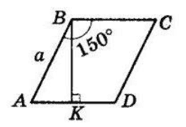
Нехай сторони квадрата і ромба дорівнюють a см.
Площа квадрата $S_1 = a^2$ см2.
В ромбі $ABCD\ ∠A =$
$= 180° – ∠B = 180° – 150° =$
$= 30°.$
$BK ⊥ AD.$
З $ΔABK\ BK = AB\ sin ∠A =$
$= a\ sin 30° = \frac{a}{2}$ (см).
Площа ромба $S_2 = AD · BK = a \frac{a}{2} = \frac{a^2}{2}.$
$S_1\ ∶\ S_2\ =\ a^2∶ (\frac{a^2}{2}) = 2.$
Відповідь:
площа квадрата у 2 рази більша.
