ВПР 4 №22 Геометрія = ВПТ 10 №22 Математика
У ромб ABCD вписано коло, радіус якого 8 см. K – точка дотику кола до сторони AB. Знайдіть площу ромба, якщо AK : KB = 1 : 4.
Розв'язок:
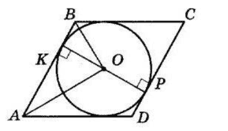
ABCD — ромб. KP — висота, K і P — точки дотику вписаного кола.
KO = OP = 8 см.
KP = 2 · 8 = 16 (см).
У ΔAOB ∠O = 90° (діагоналі перпендикулярні).
За умовою AK : KB = 1 : 4,
тоді AK = x см, KB = 4x см.
OK2 = AK · KB;
82 = x · 4x;
4x2 = 64;
x2 = 16;
x = 4 (x > 0),
AK = 4 см,
KB = 4 · 4 = 16 (см).
AB = AK + KB = 4 + 16 = 20 (см).
SABCD = AB · KP = 20 · 16 = 320 (см2).
Відповідь:
320 см2.
