№ 25.23 Геометрія = № 48.23 Математика
Більша діагональ прямокутної трапеції дорівнює 17 см, а висота – 8 см. Знайдіть площу трапеції, якщо її менша основа дорівнює 5 см.
Розв'язок:
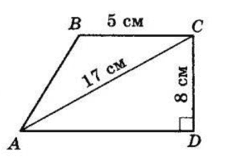
$ABCD$ — трапеція, $∠C = ∠D = 90°, $
$BC = 5$ см, $ AC = 17$ см.
З $ΔACD\ AD =$
$= \sqrt{AC^2 - CD^2} =$
$= \sqrt{17^2 - 8^2} =$
$= \sqrt{(17\ -\ 8)\ (17\ +\ 8)} =$
$= \sqrt{9 · 25} = 3 · 5 = 15$ (см).
$S_{ABCD}\ =\ \frac{BC\ +\ AD}{2}\ · CD =$
$= \frac{5 + 15}{2} · 8 = 80$ (см2).
Відповідь:
$80$ см2.
