Завдання № 25.20

№ 25.20 Геометрія =  № 48.20 Математика

У прямокутній трапеції менша основа дорівнює 6 см й утворює з меншою діагоналлю кут 45°. Знайдіть площу трапеції, якщо її тупий кут дорівнює 135°.

Розв'язок:

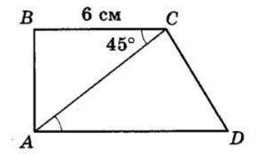
$ABCD$ — трапеція, $BC ∥ AD, BC = 6$ см.

$∠A = ∠B = 90°,$

$ ∠C = 135°, ∠BCA = 45°.$

У $ΔABC (∠B = 90°) $

$∠BCA = 45°,$

 тоді $∠BAC = 45°, $

$AB = BC = 6$ см.

$∠BCA = ∠CAD = 45° $ як внутрішні різносторонні кути при паралельних прямих $AD$ і $BC$ і січній $AC.$

У $ΔACD\ ∠ACD =$

$= ∠BCD − ∠BCA =$

$=135° − 45° = 90°. $

Тоді $∠D = 45°, AC = CD.$

З $ΔABC\ AC = \frac{AB}{sin 45°} = \frac{\sqrt2}{2} =$

$= \frac{12}{\sqrt2}$ (см),

$CD\ =\ AC\ =\ \frac{12}{\sqrt2}$ (см).

$S_{ABCD} = S_{\Delta ABC} + S_{\Delta ACD} =$

$= \frac{1}{2} AB\ · BC + \frac{1}{2} AC · CD =$

$ \frac{1}{2}·6 · 6 + \frac{1}{2} · \frac{12}{\sqrt2} · \frac{12}{\sqrt2}=$ 

$= 18 + 36 = 54$ (см²).

Відповідь:

$54$ см².