Завдання № 25.19

№ 25.19 Геометрія =  № 48.19 Математика

Знайдіть площу трапеції, основи якої дорівнюють a см і b см, а бічна сторона завдовжки c см утворює з меншою основою кут 150°.

Розв'язок:

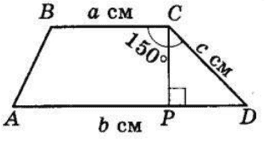
$∠D = 180° − ∠C =$

$= 180° − 150° = 30°.$

Тоді $CP = h = \frac{1}{2} $

$CD = \frac{c}{2}$ (см) (як катет,що лежить проти кута $30°$).

$S\ =\ \frac{AD\ +\ BC}{2}· h = \frac{a+b}{2} · \frac{c}{2} =$

$= \frac{(a + b)c}{4}$ (см²).

Відповідь:

$\frac{(a\ +\ b)c}{4}$ (см²).