№ 25.15 Геометрія = № 48.15 Математика
У трапеції ABCD менша основа AB дорівнює 6 см, а висота трапеції – 8 см. Знайдіть площу трапеції, якщо площа трикутника ADC дорівнює 40 см2.
Розв'язок:
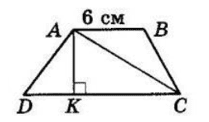
$ABCD$ — трапеція, $AB ∥ CD. AK ⊥ CD,$
$AK = 8$ см — висота трапеції, $AB = 6$ см.
$S_{\Delta ADC}\ =\ \frac{1}{2}\ CD\ · AK,$
$CD\ =\ \frac{2S_{\Delta ADC}}{AK};$
$CD\ =\frac{2 · 40}{8} = 10$ (см).
$S_{ABCD}\ =\ \frac{AB\ +\ CD}{2}\ ·AK =$
$ \frac{6 + 10}{2} · 8 = 8 · 8 = 64$ (см2).
Відповідь:
$64$ см2.
