№ 24.28 Геометрія = № 47.28 Математика
Відрізки AB і CD перетинаються в точці O, яка є серединою відрізка AB. Знайдіть відношення площ трикутників AOC і BOD, якщо CO = 3 см, DO = 6 см.
Розв'язок:
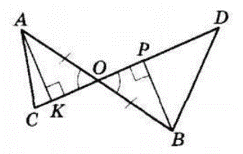
Проведемо $AK ⊥ OC, BP ⊥ OD$ — висоти трикутників $AOC$ і $BOD.$
$ΔAOK = ΔBOP$ за гіпотенузою і гострим кутом ($AO = BO$ за умовою, $∠AOK = ∠BOP$ як вертикальні).
З рівності трикутників випливає, що $AK = BP.$
$S_{\Delta AOC}\ =\ \frac{1}{2}\ CO\ · AK;$
$S_{\Delta BOD}\ =\ \frac{1}{2}\ OD\ · BP.$
$\frac{S_{\Delta AOC}}{S_{\Delta BOD}}\ = \frac{12 CO · AK}{12 OD · BP} =$
$= \frac{CO}{OD} = 1∶ 2.$
Відповідь:
1 : 2.
