№ 24.29 Геометрія = № 47.29 Математика
MN – середня лінія трикутника ABC, M ∈ AB, N ∈ AC. Знайдіть відношення площ трикутників AMN і ABC.
Розв'язок:
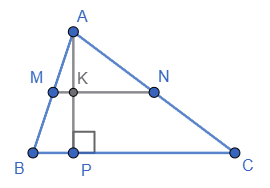
$MN$ — середня лінія
$ΔABC, MN || BC,$
$MN = \frac{1}{2} BC.$
Проведемо $AP ⊥ BC.$
Оскільки $MN || BC,$ то за теоремою Фалеса $K$ — середина $AP.$
Отже, $BC = 2MN, AP = 2AK.$
$\frac{S_{\Delta AMN}}{S_{\Delta ABC}}= \frac{\frac{1}{2}MN · AK}{\frac{1}{2}BC · AP} =$
$= \frac{MN · AK}{2MN · 2AK} – \frac{1 · 1}{2 · 2} = \frac{1}{4}.$
Відповідь:
1 : 4.
