№ 24.26 Геометрія = № 47.26 Математика
У прямокутному трикутнику точка дотику вписаного кола ділить катет на відрізки 3 см і 5 см. Знайдіть площу трикутника.
Розв'язок:
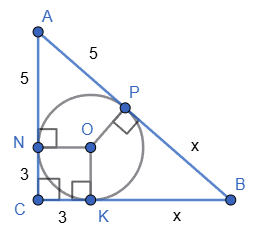
У ΔABC (∠C = 90°) N, P і K — точки дотику вписаного кола.
AN = 5 см, NC = 3 см.
ON ⊥ AC, PO ⊥ AB, OK ⊥ BC — радіуси вписаного кола.
AP = AN = 5 см, BK = NC = 3 см як відрізки дотичних до кола, проведених з однієї точки.
AC = AN + CN = 5 + 3 = 8 (см).
СNОК — квадрат (PK ⊥ CB, AC ⊥ BC, тому PK ⊥ AC; ON ⊥ AC, BC ⊥ AC, тому ON ⊥ BC).
СNОК — паралелограм з прямим кутом і рівними сусідніми сторонами, тобто квадрат.
Нехай KB = PB = x см.
Тоді AB = (x + 5) см, BC = (x + 3) см.
За теоремою Піфагора:
AB2 = AC2 + BC2,
(x + 5)2 = (x + 3)2 + 82;
x2 + 10x + 25 = x2 + 6x + 9 + 64;
10x – 6x = 73 – 25;
4x = 48;
x = 12.
Отже, BC = 3 + 12 = 15 (см).
SΔABC = $\frac{1}{2}$ AC · BC = $\frac{1}{2}$ · 8 · 15 =
= 60 (см2).
Відповідь:
60 см2.
