Завдання № 24.25

№ 24.25 Геометрія =  № 47.25 Математика

У прямокутному трикутнику точка дотику вписаного кола ділить гіпотенузу на відрізки 9 см і 6 см. Знайдіть площу трикутника.

Розв'язок:

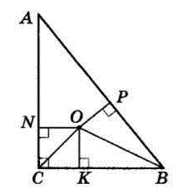
У ΔABC (∠C = 90°) N, P і K — точки дотику вписаного кола.

AP = 9 см, BP = 6 см.

ON ⊥ AC, OP ⊥ AB, OK ⊥ BC — радіуси вписаного кола.

AN = AP = 9 см, BP = 6 см як відрізки дотичних до кола, проведених з однієї точки.

СNОК — квадрат, CN = CK = x см.

Тоді AC = (x + 9) см, BC = (x + 6) см.

За теоремою Піфагора:

AB² = AC² + BC².

AB = AP + PB = 9 + 6 = 15 (см).

15² = (x + 9)² + (x + 6)²;

225 = x² + 18x + 81 + x² +

+ 12x + 36;

2x² + 30x – 108 = 0;

x² = 12x – 54 = 0;

x₁ = 3, x₂ = –18 – не задовольняє умові x > 0.

Отже, AB = 3 + 9 = 12 (см), 

BC = 3 + 6 = 9 (см).

S_Δ = $ \frac{1}{2}$ AC · BC = $ \frac{1}{2}$ · 12 · 9 =

= 54 (см²).

Відповідь:

54 см².