№ 24.24 Геометрія = № 47.24 Математика
Катети прямокутного трикутника дорівнюють 7 см і 24 см. Знайдіть висоту, проведену до гіпотенузи.
Розв'язок:
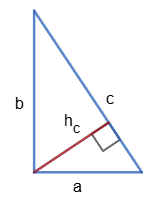
Катети трикутника $a = 7$ см, $b = 24$ см, $c$ — гіпотенуза, $h_c$ — висота, проведена до гіпотенузи.
$c = \sqrt{a^2 + b^2} =$
$= \sqrt{7^2 + 24^2} =$
$= \sqrt{49\ +\ 576} =$
$= \sqrt{625} = 25$ (см).
$S_\Delta\ =\ \frac{1}{2}\ ab\ =$
$= \frac{1}{2}\ · 7 · 24 = 84$ (см2).
$S_\Delta\ =\ \frac{1}{2}\ {ch}_c,$ звідки
$h_c = \frac{2SΔ}{c} =\frac{2 · 84}{25} = 6{,}72$ (см).
Відповідь:
$6{,}72$ см.
