Завдання № 24.22

№ 24.22 Геометрія = № 47.22 Математика

У рівнобедреному трикутнику висота, проведена до бічної сторони, ділить її на відрізки 4 см і 6 см, починаючи від вершини при основі. Знайдіть площу трикутника.

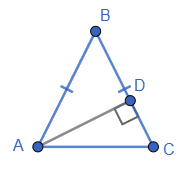
У $ΔABC\ AB = BC, $

$AD ⊥ BC,$

$ CD = 4$ см, $BD = 6$ см.

$BC = AB = BD + DC =$

$= 6 + 4 = 10$ (см).

З $ΔABD\ AD =$

$= \sqrt{AB^2 – BD^2} =$

$= \sqrt{10^2 – 6^2} =$

$= \sqrt{100 – 36} = \sqrt{64} = 8$ (см)

$(AD > 0).$

$S_{\Delta ABC}\ =\ \frac{1}{2}\ BC\ · AD =$

$= \frac{1}{2} · 10 · 8 = 40$ (см²).

$40$ см².