Завдання № 24.20

№ 24.20 Геометрія =  № 47.20 Математика

ABCD – трапеція, AD || BC. Доведіть, що S_ACD = S_ABD.

Розв'язок:

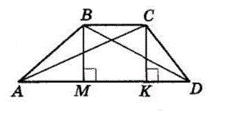
$S_{\Delta ACD}\ =\ \frac{1}{2}\ AD\ · CK,$

 де $CK ⊥ AD.$

$S_{\Delta ABD}=\ \frac{1}{2}\ AD\ · BM,$

 де $BM ⊥ AD.$

Але $CK = BM,$ як відстані між паралельними прямими $AD$ і $BC.$

Отже, $S_{ΔACD} = S_{ΔABD}.$