№ 24.19 Геометрія = № 47.19 Математика
На стороні AB трикутника ABC, площа якого дорівнює 20 см2, узято точку K так, що AK : KB = 1 : 3. Знайдіть площі трикутників ACK і CKB.
Розв'язок:
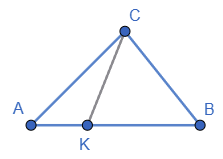
Висоти трикутників $ACK$ і $CKB$ рівні, тому
$S_{ΔACK} : S_{ΔCKB} =$
$= AK : KB = 1 : 3,$
тобто $S_{ΔCKB} = 3S_{ΔACK}.$
$S_{ΔABC} = S_{ΔACK} + S_{ΔCKB} =$
$= S_{ΔACK} + 3S_{ΔACK} =$
$= 4S_{ΔACK}.$
За умовою $4S_{ΔACK} = 20;$
$S_{ΔACK} = 5$ см2.
$S_{ΔCBK} = 3 · 5 = 15$ (см2).
Відповідь:
$5$ см2, $15$ см2.
