Завдання № 24.18

№ 24.18 Геометрія =  № 47.18 Математика

На стороні AC трикутника ABC, площа якого дорівнює 12 см², узято точку D так, що AD : DC = 1 : 2. Знайдіть площі трикутників ABD і DBC.   

Розв'язок:

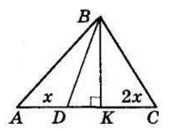
Трикутники $ABD$ і $DBC$ мають ту ж саму висоту $BK,$ проведену до прямої $AC,$ яка містить сторони $AD$ і $DC.$
Тоді площі трикутників відносяться як ці сторони.

$S_{ΔABD} : S_{ΔDBC} = 1 : 2,$

$S_{ΔDBC} = 2S_{ΔABD}.$

Оскільки $S_{ΔABD} + S_{ΔDBC} =$

$= S_{ΔABC} = 12$ см²,

то $S_{ΔABD} = 2S_{ΔABD} = 12;$

$S_{ΔABD} = 4$ (см²). 

$S_{ΔDBC} = 2 · 4 = 8$ (см²).

Відповідь:

$4$ см², $8$ см².