№ 24.10 Геометрія = № 47.10 Математика
Один з катетів прямокутного трикутника дорівнює 7 см, а гіпотенуза – 25 см. Знайдіть площу трикутника.
Розв'язок:
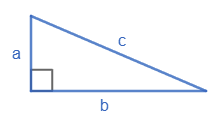
Нехай $a$ і $b$ — катети, $c$ — гіпотенуза.
$a = 7$ см, $c = 25$ см.
$a^2 + b^2 = c^2;$
$b = \sqrt{c^2 – a^2} = \sqrt{25^2 – 7^2} =$
$= \sqrt{(25 – 7)(25 + 7)} =$
$= \sqrt{18 · 32} =$
$= \sqrt{9 · 2 · 2 · 16} = $
$= \sqrt{3 · 2 · 4} = 24$ (см).
$S_\Delta\ =\ \frac{1}{2}\ ab\ =$
$= \frac{1}{2}\ · 7 · 24 = 84$ (см2).
Відповідь:
$84$ см2.
