Завдання № 23.24

№ 23.24 Геометрія =  № 46.24 Математика

Середини сторін ромба послідовно сполучено відрізками. Обчисліть площу чотирикутника, що утворився, якщо діагоналі ромба дорівнюють 6 см і 10 см.    

Розв'язок:

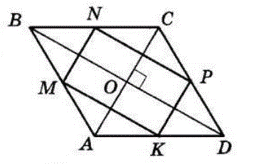
$ABCD$ — ромб, $M, N, P, K $— середини його сторін. 

$BD ⊥ AC$ як діагоналі ромба, $BD = 10$ см, $AC = 6$ см.

У $ΔABC\ MN$ — середня лінія, $MN || AC,$

$MN\ =\ \frac{1}{2}\ · AC = 12 · 6 = 3$ (см).

У $ΔACD\ PK$ — середня лінія, $PK || AC,$ 

$PK\ =\ \frac{1}{2}\ AC\ =\ \frac{1}{2}\ · 6 = 3$ см.

Тоді $MN || PK, MN = PK. $

$MNPК$ — паралелограм.

У $ΔBCD\ NP$ — середня лінія, $NP || BD,$ 

$NP\ =\ \frac{1}{2}\ BD\ =\ \frac{1}{2}\ · 10 = 5$ (см).

$MN || AC, NP || BD,$

$ AC ⊥ BD,$

тоді $MN ⊥ NP. $

$MNPK$ — прямокутник.

$S_{MNPK} = MN · NP = $

$= 3 · 5 = 15$ (см²)

Відповідь:

$15$ см².