№ 23.20 Геометрія = № 46.20 Математика
Висоти паралелограма дорівнюють 8 см і 6 см, а кут між ними – 30°. Знайдіть площу паралелограма.
Розв'язок:
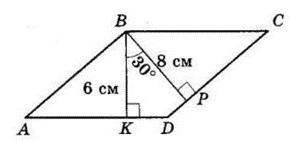
$BK ⊥ AD, BK = 6$ см;
$BP ⊥ CD, BP = 8$ см,
$∠KBP = 30°.$
У чотирикутнику $KBPD$
$∠K + ∠B + ∠P + ∠D =$
$= 360°;$
$90° + 30° + 90° + ∠D = $
$= 360°;$
$∠D = 150°.$
Тоді $∠A = ∠C = 180° − ∠D =$
$= 180° − 150° = 30°.$
З $ΔABK\ AB = 2BK =$
$= 2 · 6 = 12$ (см).
$CD = AB = 12$ см.
$S_{ABCD} = CD · BP =$
$= 12 · 8 = 96$ (см2).
Відповідь:
$96$ см2.
