№ 23.18 Геометрія = № 46.18 Математика
Дві сторони паралелограма дорівнюють 8 см і 12 см, а сума двох його висот, проведених з однієї вершини, дорівнює 15 см. Знайдіть площу паралелограма.
Розв'язок:
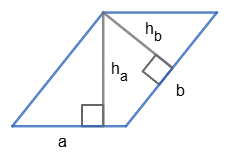
Нехай $a = 8$ см,
$b = 12$ см, $h_a = x$ см,
тоді $h_b = (15 − x)$ см.
$S_1 = ah_a = 8x$ (см2);
$S_2 = bh_b = 12(15 − x)$ (см2).
$S_1 = S_2, 8x = 12(15 − x);$
$8x = 180 − 12x; $
$20x = 180; $
$x = 9.$
Отже, $h_a = 9$ см.
$S = 8 · 9 = 72$ (см2).
Відповідь:
$72$ см2.
