№ 23.17 Геометрія = № 46.17 Математика
Периметр ромба дорівнює P см. Знайдіть його площу, якщо одна з діагоналей ромба утворює зі стороною кут 75°.
Розв'язок:
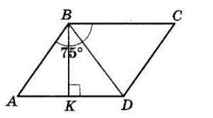
У ромбі $ABCD\ 4AB = P$ см.
Тоді $AB = BC = CD = AD = \frac{P}{4}.$
У $ΔABD\ ∠ABD = 75°,$
тоді $∠ADB = 75°,$
$∠A = 180° − 2 · 75° = 30°.$
Проведемо $BK ⊥ AD$ — висоту ромба.
У $ΔABK\ BK = \frac{1}{2}AB =$
$= \frac{1}{2} · \frac{P}{4} = \frac{P}{8}$ (см).
$\ S_{ABCD}=\ BK\ · AD =$
$= \frac{P}{8} · \frac{P}{4} = \frac{P^2}{32}$ (см2).
Відповідь:
$\frac{P^2}{32}$ см2.
